Union-Findとは
Union-Findは集合を管理するアルゴリズムです。
Union-Findをpythonで実装
実装コード
pythonでUnion-Findを実装したコードです。
競技プログラミングで使う時はコピペするかスニペット等に登録しておきます。
class UnionFind():
def __init__(self, n):
self.n = n
self.parents = [-1] * n
def find(self, x):
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self, x, y):
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
def size(self, x):
return -self.parents[self.find(x)]
def same(self, x, y):
return self.find(x) == self.find(y)
def members(self, x):
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
def roots(self):
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self):
return len(self.roots())
def all_group_members(self):
return {r: self.members(r) for r in self.roots()}
def __str__(self):
return '\n'.join('{}: {}'.format(r, self.members(r)) for r in self.roots())
コンストラクタとメソッドの説明
コンストラクタ
実装コードのコンストラクタで、引数は集合の要素の数です。
def __init__(self, n):
self.n = n
self.parents = [-1] * nfind()メソッド
「親を検索するメソッド」を再帰処理することで根を求めるメソッドです。
自分の親\( \ne \)根の場合、self.parents[x] = self.find(self.parents[x])で自分の親\( =\)根とすることで木構造が深くならないようにして、計算量を削減しています。
直接このメソッドを呼び出すことはあまりありません。
def find(self, x):
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
pythonは再帰処理が遅いことで有名ですが、実装コードでは再帰処理(木構造)が深くならないように処理しているので問題ありません。
union()メソッド
集合の要素を結合するメソッドです。
def union(self, x, y):
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
処理内容は次のようになっています。
union()メソッドの処理内容
- 引数
xとyの根を検索 - 根が同じなら処理なし
- 根が違う場合には要素数の多いグループの根に結合
self.parents[x] += self.parents[y]
self.parents[y] = xここが処理がポイントで、self.parents[x] += self.parents[y]で集合の要素数を根に保持し、self.parents[y] = xで要素の根を管理しています。
size()メソッド
集合の要素数を求めるメソッドです。
集合の要素数は根が保持しているので、その値を返しています。
def size(self, x):
return -self.parents[self.find(x)]same()メソッド
\(2\)つの要素が同じグループかどうか確認するメソッドです。
グループが同じ場合には根が同じとなるので、各引数のねが同じかどうかを返しています。
def same(self, x, y):
return self.find(x) == self.find(y)
members()メソッド
引数の要素に属する要素を全て返します。
def members(self, x):
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
roots()メソッド
各グループの根を返します。
def roots(self):
return [i for i, x in enumerate(self.parents) if x < 0]
group_count()メソッド
グループの数\(=\)根の数なのでroots()メソッドの配列の大きさを返します。
def group_count(self):
return len(self.roots())
all_group_members()メソッド
全てのグループの根と要素を返します。
def all_group_members(self):
return {r: self.members(r) for r in self.roots()}使い方
インスタンス化
クラスを使う際にはまずは、クラスをインスタンス化する必要があるので次のようにインスタンスを作成します。
uf = UnionFind(4)引数は集合の要素の数なので、集合の要素が\(4\)のクラスが作成されます。
初期状態では各要素は自分自身が根となっています。
print(uf)で各グループの根と要素を出力すると次のようになります。
0: [0]
1: [1]
2: [2]
3: [3]集合の要素の結合
Union-Findで最も利用頻度が高いメソッドです。
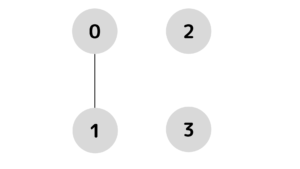
要素\(0\)と\(1\)を連結してみます。
uf.union(0, 1)結合後はどうなっているのでしょうか?
print(uf)で各グループの根と要素を出力すると次のようになります。
0: [0, 1]
2: [2]
3: [3]要素\(0\)と\(1\)が連結されて同じグループになったことが確認できます。
根が\(0\)でそこに\(1\)が結合されていることが分かります。
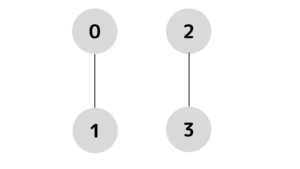
どんどん結合してみましょう。
uf.union(2, 3)0: [0, 1]
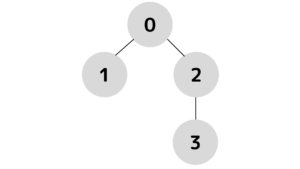
2: [2, 3]uf.union(0, 2)0: [0, 1, 2, 3]要素同士が結合されていく様子が分かります。
集合の要素数を出力する
各要素に含まれる要素数を出力する場合は次のようにします。
print(uf.size(3))4「集合の要素を連結」で全ての要素が結合されていますので、\(4\)が出力されました。