問題概要
問題ページ
-
-
D - 徒競走
問題ページへ移動する
問題文
\(N\) 匹のうさぎがいます。 うさぎは \(1\) から \(N\) まで番号が振られています。
これら \(N\) 匹のうさぎが徒競走をしました。 同着はいませんでした。 このとき、着順は \(N!\) 通り考えられます。
高橋君は \(M\) 人の観客から情報を集めました。 \(i\) 番目の観客によると、うさぎ \(x_i\) はうさぎ \(y_i\) よりも先にゴールしたそうです。
すべての観客の情報に合致するような着順が何通り考えられるか求めてください。
制約
- \(2≦N≦16\)
- \(1≦M≦N(N-1)/2\)
- \(1≦x_i,y_i≦N\)
- \(x_i≠y_i\)
- \((x_i,y_i)\) の組はすべて相異なる。
- すべての観客の情報に合致するような着順が少なくともひとつ存在する。
部分点
- \(30\) 点分のテストケースでは、\(N≦8\) を満たす。
問題の考察
トポロジカルソートの数え上げの問題。
全列挙による数え上げだと計算量が\(O(2^N)\)なので間に合わない。
BitDPを使えば\(O(2^N \times N)\)に計算量を抑えることができる。
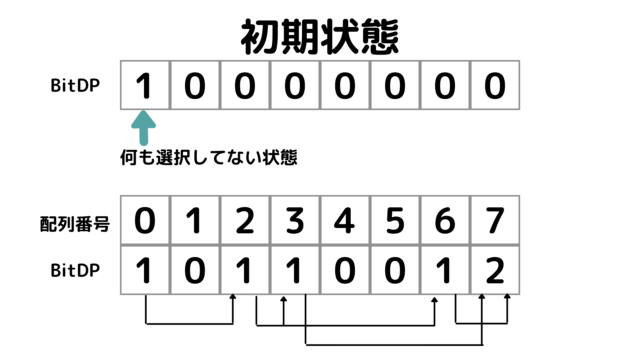
「例題1」のBiT遷移のイメージは次のようになります。
BitDPの初期状態は「何も選択してない状態」が\(1\)つある状態です。
そこから移動元のBitの個数を移動先のBitへ足していきます。
このように計算すると、現時点で既に並び替えに使用している数字の内、使用した数字が同じ(例えば使用済が\((1,2)\)と\((2,1))\)で残りが\(3,4,5\)で共通なものなど)組み合わせについてはまとめて計算してしまうことでできるので大幅に計算量を削減することができます。
さて、この問題のポイントとなるトポロジカルソートの数え上げの方法ですが次のように考えます。
トポロジカルソートの数え上げ
- 現在のBit(
i)から遷移先のBit(j)を全検索 - 遷移先のBit(
bt_list[j])は現在Bitで未使用 - 並び替え順で、遷移先のBitより後でなければならないBit(
next_list)は未使用
この問題(トポロジカルソートの数え上げ)のポイントは、移動先のBitだけでなく、移動先のBitより並び替え順で後になるBitが全て未使用かどうか確認する必要があるというところです。
これは、最初の\((x_i,y_i)\) の読込の時点でnext_listとしてBitリストを作成しておきます。
全検索の際に、i & bt_list[j] == 0で移動先のBitが未使用か、i & next_list[j] == 0で移動先のBitより並び替え順の後になるBitが全て未使用かどうか確認しています。
まずは解説をよく読んで理解した後に、自分自身でコーディングをして知識の定着を確認しましょう!
ACコード
import sys
def solve():
input = sys.stdin.readline
mod = 10 ** 9 + 7
n, m = list(map(int, input().rstrip('\n').split()))
next_list = [0] * n
for i in range(m):
x, y = list(map(int, input().rstrip('\n').split()))
next_list[y - 1] |= 1 << (x - 1)
bt_list = [1 << i for i in range(n)]
dp = [0] * (1 << n)
dp[0] = 1
for i in range(1 << n):
for j in range(n):
if i & bt_list[j] == 0 and i & next_list[j] == 0:
dp[i + bt_list[j]] += dp[i]
print(dp[-1])
if __name__ == '__main__':
solve()