問題概要
問題ページ
-
-
D - Decayed Bridges
問題ページへ移動する
問題文
\(N\) 個の島と \(M\) 本の橋があります。
\(i\) 番目の橋は \(A_i\) 番目の島と \(B_i\) 番目の島を繋いでおり、双方向に行き来可能です。
はじめ、どの \(2\) つの島についてもいくつかの橋を渡って互いに行き来できます。
調査の結果、老朽化のためこれら \(M\) 本の橋は \(1\) 番目の橋から順に全て崩落することがわかりました。
「いくつかの橋を渡って互いに行き来できなくなった \(2\) つの島の組 \((a, b)\) (\(a < b\)) の数」を不便さと呼ぶことにします。
各 \(i\) \((1 \leq i \leq M)\) について、\(i\) 番目の橋が崩落した直後の不便さを求めてください。
制約
- 入力は全て整数である。
- \(2 \leq N \leq 10^5\)
- \(1 \leq M \leq 10^5\)
- \(1 \leq A_i < B_i \leq N\)
- \((A_i, B_i)\) の組は全て異なる。
- 初期状態における不便さは \(0\) である。
問題の考察
最初に\(M\)本の橋で島が連結されている状態から、順番に橋が崩落していく。
橋を経由して往来ができなくなっている島のペアの数を「不便さ」として、各時点における「不便さ」を求める問題。
どのような状態か例題1で考えてみる。
例題1の遷移
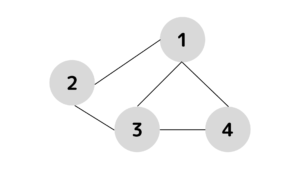
初期状態
この時点の不便さは\(0\)
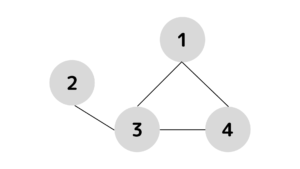
1つ目の橋が崩落
この時点の不便さは\(0\)
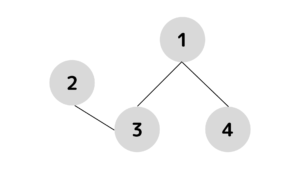
2つ目の橋が崩落
この時点の不便さは\(0\)
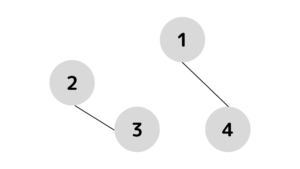
3つ目の橋が崩落
この時点で初めて往来ができなくなる島が発生し、\((1,2),(1,3),(2,4),(3,4)\)の\(4\)ペアの島で往来ができなくなる。
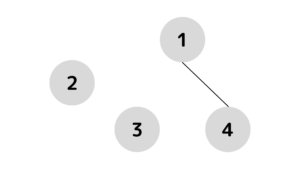
4つ目の橋が崩落
\(1\)つ前の状態に加えて\((2,3)\)のペアで島の往来ができなくなる。
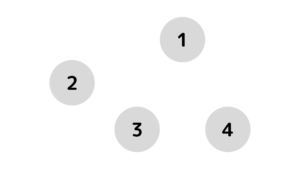
最後の橋が崩落
\(1\)つ前の状態に加えて\((1,4)\)のペアで島の往来ができなくなる。
逆から考える
この問題は橋で連結されている状態から各橋が崩落するという問題文通りに考えると難しい。
「橋が全て崩落している状態から、逆順で橋を連結していく」と考えることができれば、Union-Findを使って解くことができる。
-

-
【python/アルゴリズム】Union-Findを基礎から解説
続きを見る
連結する\(2\)つの島の連結成分の数だけ不便さが解消されていることが分かる。
「\(4\)つ目の橋が崩落」→「\(4\)つ目の橋が崩落」では\(2,3\)の島の連結成分はそれぞれ\(1\)(\((2),(3)\))なので\(1 \times 1 = 1\)だけ不便さが解消される。
「\(3\)つ目の橋が崩落」→「\(2\)つ目の橋が崩落」では\(1,3\)の島の連結成分はそれぞれ\(2\)(\((1,4),(3,2)\))なので\(2 \times 2 = 4\)だけ不便さが解消される。
という風に考えて行けばよい。
問題の考え方
- 全ての橋が崩落している状態から逆順で考える
- 初期状態の不便さは\(N \times (N - 1) \div 2\)
- 橋が連結された時は、連結される橋の連結成分から解消される不便さを求める
- 解消される不便さは、\(連結される橋の連結成分 \times 連結される橋の連結成分\)
橋の連結についてはUnion-Findを使うことでほぼ定数倍の計算量で処理することができるのでpythonでも十分に間に合う。
-
-
1693
続きを見る
Union-Findは競プログラミングで頻出なのでライブラリに登録して使えるようにしておきましょう!
ACコード
import sys
class UnionFind():
def __init__(self, n):
self.n = n
self.parents = [-1] * n
def find(self, x):
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def size(self, x):
return -self.parents[self.find(x)]
def same(self, x, y):
return self.find(x) == self.find(y)
def members(self, x):
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
def roots(self):
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self):
return len(self.roots())
def all_group_members(self):
return {r: self.members(r) for r in self.roots()}
def __str__(self):
return '\n'.join('{}: {}'.format(r, self.members(r)) for r in self.roots())
def solve():
input = sys.stdin.readline
mod = 10 ** 9 + 7
n, m = list(map(int, input().rstrip('\n').split()))
ab = [list(map(int, input().rstrip('\n').split())) for _ in range(m)]
uf = UnionFind(n)
ab.reverse()
cnt = (n - 1) * n // 2
res = []
for a, b in ab:
res.append(cnt)
if not uf.same(a - 1, b - 1):
cnt -= uf.size(a - 1) * uf.size(b - 1)
uf.union(a - 1, b - 1)
res.reverse()
print(*res, sep="\n")
if __name__ == '__main__':
solve()