【pythonでABC156を解説】B - Digits

問題概要

問題ページ

B - Digits

問題ページへ移動する

問題文

整数 \(N\) を \(K\) 進数で表したとき、何桁になるかを求めてください。

注記

\(K\) 進表記については、Wikipedia「位取り記数法」を参照してください。

制約

• 入力は全て整数である。
• \(1 \leq N \leq 10^9\)
• \(2 \leq K \leq 10\)

問題の考察

B問題にしては難しめな問題です。

まずは実際に10進数を実際に各\(K\)進数にしてみましょう。

\(N\)進数への変換方法はこちらを参考にしてください。

 

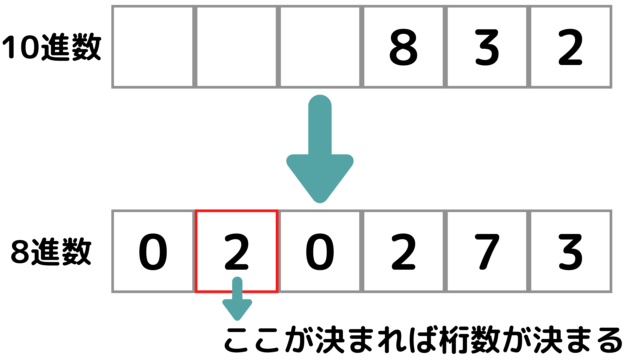
桁数が何桁になるかを考えなければいけないのですが、\(K\)進数の桁数は最上位桁が決まれば決定します。

上位から考えて初めて\(0\)以外が出現した時に最上位桁が決定していきます。

この画像では\(6\)桁目のボックスに\(0\)が入っていますが、\(020273\)ではなく\(20273\)が\(8\)進数に変換した時の表記となります。

実際に\(K\)進数に変換する方法としては、「最上位桁数から決定する」と「最下位桁数から決定する」の二つの考え方があります。

 

ACコード

最下位桁から求める

import sys


def solve():
    input = sys.stdin.readline
    mod = 10 ** 9 + 7
    n, k = list(map(int, input().rstrip('\n').split()))
    cnt = 0
    while n != 0:
        n, m = divmod(n, k)
        cnt += 1
        #cnt桁目はm
    print(cnt)


if __name__ == '__main__':
    solve()

最上位桁から求める

import sys


def solve():
    readline = sys.stdin.buffer.readline
    mod = 10 ** 9 + 7
    n, k = list(map(int, readline().split()))
    for i in range(10 ** 10):
        if pow(k, i) > n:
            for j in range(i, -1, -1):
                p = pow(k, j)
                if n // p != 0:
                    #(j + 1)桁目は(n // p)
                    print(j + 1)
                    exit()
            exit()


if __name__ == '__main__':
    solve()