問題概要
問題ページ
-
-
C - Travel
問題ページへ移動する
問題文
\(N\) 個の都市があります。都市 \(i\) から都市 \(j\) へ移動するには \(T_{i,j}\) の時間がかかります。
都市 \(1\) を出発し、全ての都市をちょうど \(1\) 度ずつ訪問してから都市 \(1\) に戻るような経路のうち、移動時間の合計がちょうど \(K\) になるようなものはいくつありますか?
制約
- \(2\leq N \leq 8\)
- \(i\neq j\) のとき \(1\leq T_{i,j} \leq 10^8\)
- \(T_{i,i}=0\)
- \(T_{i,j}=T_{j,i}\)
- \(1\leq K \leq 10^9\)
- 入力はすべて整数
問題の考察
経路のパターンを全検索する問題。
制約が\(2\leq N \leq 8\)なので全ての並びを計算しても\( {}_n P_n =n!\)となり計算量は\(40,000\)程度なので間に合う。
pythonで順列を扱う時には、itertools.permutationsを使うのが楽。
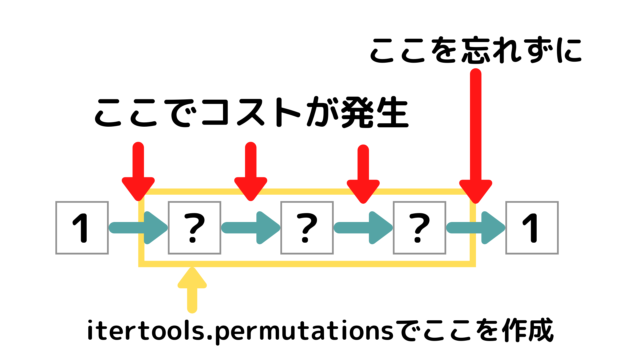
今回は\(1\)からスタートして各点を\(1\)回ずつ訪問すると問題になるので、\(2\)から\(N\)までを作成すると良い。
配列の添え字の関係で実際は、\(2-1\)から\(N-1\)を作成する。
イメージは次の図の通り。
各順列毎にコストの合計を計算して、これが\(K\)に一致するパターンの個数をカウントする。
コーディングする際に、最後に\(1\)に戻る部分を忘れないようにしたい。
ACコードでは、for v in it_vで\(1\)から各頂点への訪問順序を、if k == cost + t[lp][0]:で判定の際に\(1\)へ戻るコストを加算している。
たびすけ
itertools.permutationsは使い方を知っていると便利です。C問題では
itertools.permutationsを使う問題が定期的に出題されています!ACコード
import sys
import itertools
def solve():
input = sys.stdin.readline
mod = 10 ** 9 + 7
n, k = list(map(int, input().rstrip('\n').split()))
t = [list(map(int, input().rstrip('\n').split())) for _ in range(n)]
cnt = 0
for it_v in itertools.permutations(range(1, n)):
cost = 0
lp = 0
for v in it_v:
cost += t[lp][v]
lp = v
if k == cost + t[lp][0]:
cnt += 1
print(cnt)
if __name__ == '__main__':
solve()