ABC解説

【pythonでABC188を解説】C - ABC Tournament

問題概要

問題ページ

C - ABC Tournament
C - ABC Tournament

問題ページへ移動する

問題文

選手 \(1\) から選手 \(2^N\) までの \(2^N\) 人の選手がトーナメント形式のプログラミング対決をします。
選手 \(i\) のレートは \(A_i\) です。どの \(2\) 人の選手のレートも異なり、\(2\) 人の選手が対戦すると常にレートが高い方が勝ちます。

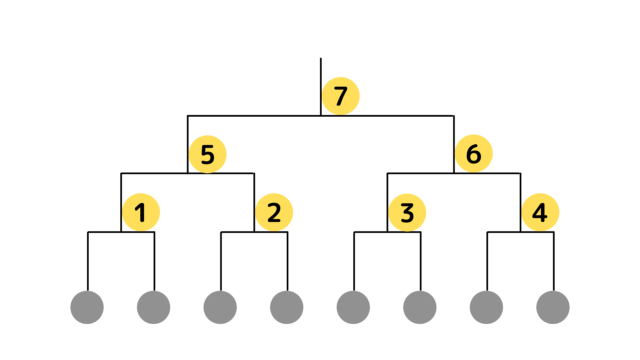
トーナメント表は完全二分木の形をしています。
より正確には、このトーナメントは以下の要領で行われます。

  • \(i = 1, 2, 3, \dots, N\) について順に、以下のことが行われる。
    • 各整数 \(j (1 \le j \le 2^{N - i})\) について、まだ負けたことのない選手のうち、 \(2j - 1\) 番目に番号の小さい選手と \(2j\) 番目に番号の小さい選手が対戦する。

準優勝する、すなわち最後に行われる対戦において負ける選手の番号を求めてください。

制約

  • \(1 \le N \le 16\)
  • \(1 \le A_i \le 10^9\)
  • \(A_i\) は相異なる
  • 入力に含まれる値は全て整数である

問題の考察

トーナメントの準優勝者を求める問題。

イメージはこんな感じです。

優勝者を求める問題だと、max()とfor文で簡単に解けるので難易度が1段階下がる。

少し考えると、「準優勝者」\( \ne\)「レートが\(2\)番目に高い選手」ということに気づく。

レートが\(2\)番目に高い選手が決勝前にレートが\(1\)番高い選手と対戦する場合、準優勝者が\(2\)番目にレートが高い選手にならない。

問題文の通りに処理すれば、計算量は\(O(\log 2^N \times 2^N \div 2)\)以下なので十分に間に合う。

処理手順

  • リストの先頭から\(2\)要素取り出す
  • レートの高い方をリストの末尾に追加
  • （繰返し）
  • 最後に\(2\)要素のレートが低い方を出力

 

この手順で処理する場合、listだと間に合わないので、双方向リストのcollection.deque()を使います。

たびすけ
たびすけ
deque()は競プロ頻出の幅優先探索でも使うので覚えておきましょう！

ACコード

import sys
import collections


def solve():
    input = sys.stdin.readline
    mod = 10 ** 9 + 7
    n = int(input().rstrip('\n'))
    a = collections.deque()
    for i, v in enumerate(list(map(int, input().rstrip('\n').split()))):
        a.append([i, v])
    while len(a):
        xi, xv = a.popleft()
        yi, yv = a.popleft()
        if xv < yv:
            xi, yi = yi, xi
            xv, yv = yv, xv
        if len(a) == 0:
            print(yi + 1)
        else:
            a.append([xi, xv])


if __name__ == '__main__':
    solve()

-ABC解説
-,