【pythonでABC153を解説】D - Caracal vs Monster

問題概要

問題ページ

問題文

カラカルはモンスターと戦っています。

モンスターの体力は \(H\) です。

カラカルはモンスターを \(1\) 体選んで攻撃することができます。モンスターを攻撃したとき、攻撃対象のモンスターの体力に応じて、次のどちらかが起こります。

• モンスターの体力が \(1\) なら、そのモンスターの体力は \(0\) になる
• モンスターの体力が \(X >1\) なら、そのモンスターは消滅し、体力が \(\lfloor X/2 \rfloor\) のモンスターが新たに \(2\) 体現れる

（\(\lfloor r \rfloor\) は \(r\) を超えない最大の整数を表す）

全てのモンスターの体力を \(0\) 以下にすればカラカルの勝ちです。

カラカルがモンスターに勝つまでに行う攻撃の回数の最小値を求めてください。

制約

• \(1 \leq H \leq 10^{12}\)
• 入力中のすべての値は整数である。

問題の考察

深さ優先探索で解ける問題。

適当な数字でどうなるかを確認してみる。

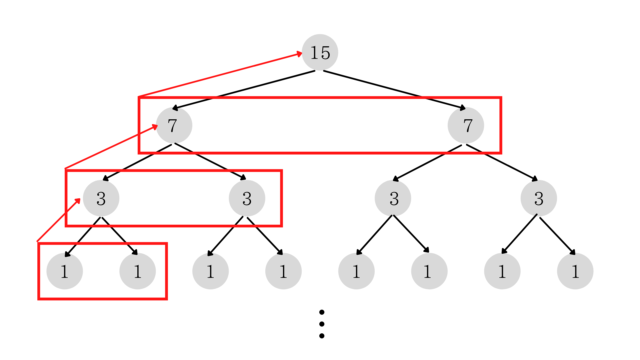
\(H\)が\(15\)の場合には次のようになる。

階層の深さが\(\log H\)で、階層が\(1\)深くなる毎に計算量は\(2\)倍になっていく。

つまり、愚直に計算すると計算量は\(O(2^{\log N})\)となり、\( H = 10^{12}\)の時を考えると間に合わない。

たびすけ

解法が「深さ優先探索」っぽいけど間に合わなさそうだったので、「メモ化再帰」を使って解答しました。

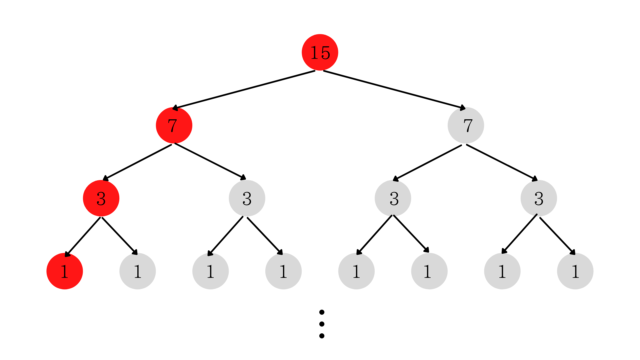
しかし、よく考えてみると同階層の値は全て同じ（例の場合は、\(3\)階層目の値は全て\(3\)となっている）なので、メモ化しなくても同等の計算量に削減できる。

攻撃回数ベースで考えると次の図のようになっていることが分かる。

\(1\)階層上の階層の攻撃回数は\(=\)\(1\)階層下の攻撃回数\(\times 2 + 1\)となっていることが分かる。

つまり、赤くなっている部分だけ計算すれば全体で必要な攻撃回数が求められます。

この場合、計算量は\( H = 10^{12}\)の時も\(O(40)\)程度でpythonであっても十分に間に合う。

たびすけ

メモ化再帰を使ってもいいし、深さ優先探索で\(1\)階層上の階層の攻撃回数は\(=\)\(1\)階層下の攻撃回数\(\times 2 + 1\)を使って計算しても解答できます。

ACコード

実際に提出したコード

import sys
from functools import lru_cache


@lru_cache(maxsize=None)
def alg_memoization_recursion(n):
    if n == 1:
        return 1
    else:
        return alg_memoization_recursion(n // 2) + alg_memoization_recursion(n // 2) + 1


def solve():
    input = sys.stdin.readline
    mod = 10 ** 9 + 7
    h = int(input().rstrip('\n'))
    print(alg_memoization_recursion(h))


if __name__ == '__main__':
    solve()

メモ化なしの再帰コード

import sys


def func(n):
    if n == 1:
        return 1
    else:
        return func(n // 2) * 2 + 1


def solve():
    input = sys.stdin.readline
    mod = 10 ** 9 + 7
    h = int(input().rstrip('\n'))
    print(func(h))


if __name__ == '__main__':
    solve()

再起なしのコード

import sys
import collections


def solve():
    input = sys.stdin.readline
    mod = 10 ** 9 + 7
    h = int(input().rstrip('\n'))
    ql = [h]
    d = collections.defaultdict(int)
    d[0] = 0
    while len(ql):
        vl = ql[-1]
        if vl // 2 in d:
            d[vl] = d[vl // 2] * 2 + 1
            ql.pop()
        else:
            ql.append(vl // 2)
    print(d[h])


if __name__ == '__main__':
    solve()