【pythonでABC188を解説】D - Snuke Prime

問題概要

問題ページ

D - Snuke Prime

問題ページへ移動する

問題文

株式会社すぬけは様々なサービスを提供しています。
この会社は、すぬけプライムという支払いプランを用意しています。
すぬけプライムへの加入中は、\(1\) 日あたり \(C\) 円を支払うことで、提供される全てのサービスを追加料金の支払いなしに利用することができます。
すぬけプライムへの加入および脱退は、それぞれ \(1\) 日の始めおよび終わりに自由に行うことができます。

高橋くんは、この会社のサービスのうち \(N\) 個を利用しようとしています。
そのうち \(i\) 個目のサービスは、今日を \(1\) 日目として、\(a_i\) 日目の始めから \(b_i\) 日目の終わりまで利用する予定です。
すぬけプライムに加入していない期間中は、\(i\) 個目のサービスを利用する際に \(1\) 日あたり \(c_i\) 円を支払う必要があります。

サービスを利用するために高橋くんが支払う必要のある最小の合計金額を求めてください。

制約

• \(1 \leq N \leq 2 \times 10^5\)
• \(1 \leq C \leq 10^9\)
• \(1 \leq a_i \leq b_i \leq 10^9\)
• \(1 \leq c_i \leq 10^9\)
• 入力に含まれる値は全て整数

問題の考察

imos法っぽい問題。

制約が\(1 \leq a_i \leq b_i \leq 10^9\)なので、テンプレのimos法だと間に合わない。

\(1 \leq N \leq 2 \times 10^5\)なので、同一コスト区間の座標を圧縮して考えれば間に合う。

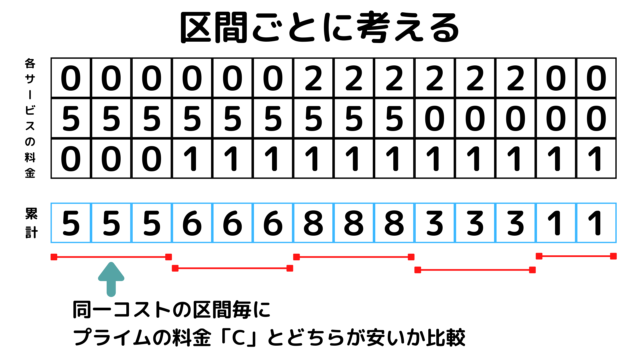
区間の総コストは次の式で計算できる。

min\((C,\)区間コスト\() \times\)区間の要素数。

画像で\(C\)が\(4\)の場合を考える。

総コストは

\(min(4,5) \times 3 \)\(+min(4,6) \times 3 \)\(+min(4,8) \times 3 \)\(+min(4,3) \times 3 \)\(+min(4,1) \times 2 \)\(=16\)

となります。

座標を圧縮する方法色々あるが、ACコードでは次のように考えている。

dを昇順に並び替えることで、区間の先頭から順に処理することができます。

imos法の考え方は次の部分。

for i in range(n):
    a, b, c = list(map(int, input().rstrip('\n').split()))
    d[a] += c
    d[b + 1] -= c

d[b + 1] -= cがこの問題のポイントです。

ACコード

import sys
import collections


def solve():
    input = sys.stdin.readline
    mod = 10 ** 9 + 7
    n, C = list(map(int, input().rstrip('\n').split()))
    d = collections.defaultdict(int)
    for i in range(n):
        a, b, c = list(map(int, input().rstrip('\n').split()))
        d[a] += c
        d[b+1] -= c
    ac = 0
    lst = 0
    total = 0
    for k, v in sorted(d.items()):
        if lst != 0:
            total += (k - lst) * min(C, ac)
        ac += v
        lst = k
    print(total)


if __name__ == '__main__':
    solve()