問題概要
問題ページ
-
-
E - Peddler
問題ページへ移動する
問題文
高橋国には、町 \(1\) から町 \(N\) までの \(N\) 個の町があります。
また、この国には道 \(1\) から道 \(M\) までの \(M\) 本の道があります。道 \(i\) を使うと、町 \(X_i\) から町 \(Y_i\) へ移動することができます。逆向きへは移動できません。ここで \(X_i < Y_i\) であることが保証されます。
この国では金の取引が盛んであり、町 \(i\) では、金 \(1\,\mathrm{kg}\) を \(A_i\) 円で売ったり買ったりすることができます。
旅商人である高橋君は、高橋国内のある町で金を \(1\,\mathrm{kg}\) だけ買い、いくつかの道を使った後、買った町とは別の町で金を \(1\,\mathrm{kg}\) だけ売ろうと考えています。
このとき、高橋君の利益 (すなわち \((\)金を売った価格\() - (\)金を買った価格\()\)) として考えられる最大値を求めてください。
制約
- \(2 \le N \le 2 \times 10^5\)
- \(1 \le M \le 2 \times 10^5\)
- \(1 \le A_i \le 10^9\)
- \(1 \le X_i \lt Y_i \le N\)
- \((X_i, Y_i) \neq (X_j, Y_j) (i \neq j)\)
- 入力に含まれる値は全て整数
問題の考察
どの町で買ってどの町で売るかについては、全ての町の組合せを試すと計算量が\((2 \times 10^5)^2\)となり間に合わない。
重要な条件
- 町 \(X_i\) から町 \(Y_i\) へ移動することができ、逆向きへは移動できません。
- ここで \(X_i < Y_i\) であることが保証されます。
この条件に着目し、\(X_i\) が小さい順に処理していけば各町\(i\)に到着するまでに購入できる一番安い金の金額が分かる。
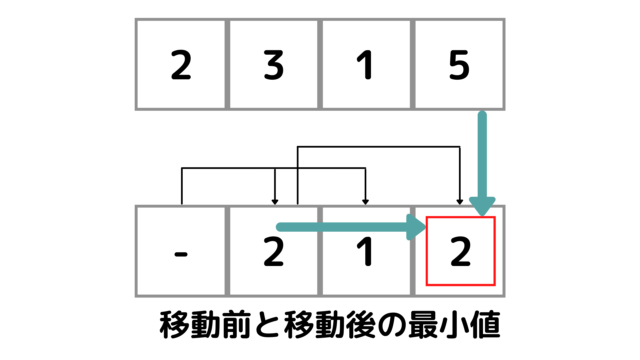
例題\(1\)だと次のような感じになる。
町\(4\)に到着するまでに買える金で最も安いものは\(2\)となる。
最も安い金の求め方
- \(X_i\)を昇順に並び替える
- dp配列を準備する(初期値は\(10^9\)以上)
- 各\(X_i,Y_i\)を順に処理
- 移動後\(Y_i\) の最小値は\(min(dp[X_i], dp[Y_i], A_{Y_i})\)
移動後\(Y_i\)の最小値は、dpテーブルの移動前、移動後、\(A\)の移動後、この\(3\)つの値の最小値となる。
これで各町に到着するまでに買える最小の金の金額が求められた。
あとは、各町\(i\)で売却額\(A_i\)と購入金額dp[\(i\)]の差額を求め、その最大値を求めれば良い。
ACコード
import sys
import collections
def solve():
input = sys.stdin.readline
mod = 10 ** 9 + 7
n, m = list(map(int, input().rstrip('\n').split()))
a = list(map(int, input().rstrip('\n').split()))
d = collections.defaultdict(list)
dp = [10 ** 10] * n
for i in range(m):
x, y = list(map(int, input().rstrip('\n').split()))
d[x-1] += [y-1]
for i in range(n):
for nt_pos in d[i]:
dp[nt_pos] = min(a[i], dp[i], dp[nt_pos])
mx = -(10 ** 10)
for i in range(n):
mx = max(mx, a[i] - dp[i])
print(mx)
if __name__ == '__main__':
solve()