【pythonでABC189を解説】D - Logical Expression

問題概要

問題ページ

問題文

\(N\) 個の文字列 \(S_1,\ldots,S_N\) が与えられます。各文字列は AND または OR です。

値が \(\text{True}\) または \(\text{False}\) であるような \(N+1\) 個の変数の組 \((x_0,\ldots,x_N)\) であって、
以下のような計算を行った際に、\(y_N\) が \(\text{True}\) となるようなものの個数を求めてください。

• \(y_0=x_0\)
• \(i\geq 1\) のとき、\(S_i\) が AND なら \(y_i=y_{i-1} \land x_i\)、\(S_i\) が OR なら \(y_i=y_{i-1} \lor x_i\)

\(a \land b\) は \(a\) と \(b\) の論理積を表し、\(a \lor b\) は \(a\) と \(b\) の論理和を表します。

制約

• \(1 \leq N \leq 60\)
• \(S_i\) は AND または OR

問題の考察

典型的なDPの問題。

まずは論理和と論理積について確認しておきましょう。

\((x_0,\ldots,x_N)\)の各値は、 \(\text{True}\) または \(\text{False}\) の数列のうち条件を満たすものを求める。

\(S_1,\ldots,S_N\)と\((x_0,\ldots,x_N)\)の組み合わせから最終的な値が\(\text{True}\)になるものを求めれば良い。

全パターンを試そうとすると、計算量が\(O(2^N)\)になり、制約が\(1 \leq N \leq 60\)のため間に合わないことが分かる。

この条件から次のことが分かる。

この形をDPに落とし込めば高速に解答することができる。

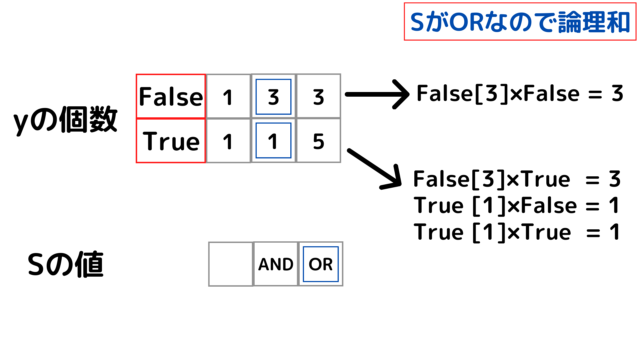
入力例\(1\)のDPテーブルは次のようになっている。

青枠で囲われた部分から最後尾のテーブルを埋めることができる。

図のようにyの個数は\(y_{i-1}\)と\(S_i\)から求めることができる。

\(x_i\)は、\(\text{True}\) と \(\text{False}\)の両方の組み合わせを試せばよい。

この方法であれば、\(O(N)\)で答えを求めることができる。

たびすけ

典型的なDPだけど論理演算も含まれるので少し難しく見えるかも。。。
DPテーブルの初期値は\(\text{True}\) と \(\text{False}\)が\(1\)つずつ存在しますので忘れずに！

ACコード

import sys


def solve():
    input = sys.stdin.readline
    mod = 10 ** 9 + 7
    n = int(input().rstrip('\n'))
    s = [str(input().rstrip('\n')) for _ in range(n)]
    dp = [[0] * 2 for _ in range(n + 1)]
    dp[0][0] = 1
    dp[0][1] = 1
    #各桁
    for i in range(1, n + 1):
        #求める桁の1つ手前の桁のTrue、False
        for j in range(2):
            #求める桁のxのTrue、False
            for k in range(2):
                #S、1つ手前の桁、xから結果がTrue、Falseか計算
                y = j & k if s[i-1] == "AND" else j | k
                #1つ前の桁の個数を計算結果へ加算
                dp[i][y] += dp[i-1][j]
    print(dp[-1][1])


if __name__ == '__main__':
    solve()